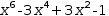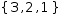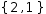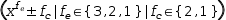3.4.6 Factor

Polynomial Factor rewrites a subject polynomial with non-negative exponents and integer coefficients as a product of linear polynomials that have integer roots or quadratic factors that may have roots. If the result after application is unchanged from the subject it is because no factors could be found. This could be because there are no integer roots or because the roots are complex. In the former case, a factor can be found using Newton and Factor can proceed from the result of that transformation.

Factor finds integer roots in most cases where they exist. A quadratic factor is left as such even though it may have integer roots.

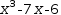
• The factors of x^3-7⋅x-6 are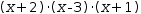 (x+2)⋅(x-3)⋅(x+1). The factoring consists of monic linear polynomials that represent roots at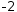 -2,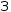 3 and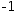 -1.
• The factors of x^4-1 include a quadratic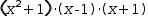 (x^2+1)⋅(x-1)⋅(x+1) which has no real roots. They can be found using Quadratic and shown to be imaginary: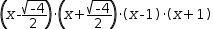 (x-√(-4)÷2)⋅(x+√(-4)÷2)⋅(x-1)⋅(x+1).
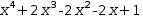
• Even if the quadratic has real roots, it is left in quadratic form. That is, x^4+2⋅x^3-2⋅x^2-2⋅x+1 factors to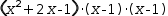 (x^2+2⋅x-1)⋅(x-1)⋅(x-1) even though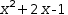 x^2+2⋅x-1 has real roots. These can be found by Quadratic ; the final factoring is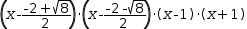 (x-(-2+√8)÷2)⋅(x-(-2-√8)÷2)⋅(x-1)⋅(x+1).
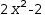
• Finally, linear roots are not necessarily monic. 2⋅x^2-2 factors to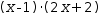 (x-1)⋅(2⋅x+2). The monic form can be found by applying the fast-action Factor to produce the product of linear monics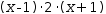 (x-1)⋅2⋅(x+1).

Factors are found by generating a set of trial factors from the subject and applying polynomial division to produce a quotient and a remainder. If the remainder is zero, the trial factor is an actual factor. Transformation continues by factoring the quotient as the new subject. If the trial factor is cubic or higher it is factored as well.

Trial factors are generated from integer factors (including 1) of the leading exponent and the constant coefficient. For example, the expression x^6-3⋅x^4+3⋅x^2-1 has a leading exponent of 6 (with factors {3, 2, 1}) and a constant coefficient of 2 (with factors {2, 1}). Trial factors are generated from the expression (x^f_e±f_c|f_e∈{3, 2, 1}|f_c∈{2, 1}).